Bimbel Jakarta Timur akan membahas mengenai Menghitung Luas Segi-n Beraturan Dengan Trigonometri. Segi-n beraturan yaitu bangun datar atau bentuk dimensi 2 yang terdiri dari garis-garis bersambungan membentuk bangun tertutup dengan sisi yang sama panjang dan sudut yang sama besar.
Jumlah besar sudut dalam segi-n beraturan dapat ditentukan dengan rumus :
contoh :
- Jumlah besar sudut dalam segitiga =(3-2) x 180°= 180°
- Jumlah besar sudut dalam segiempat =(4-2) x 180°=360°
- Jumlah besar sudut dalam segilima =(5-2) x 180°=540°
Jumlah besar setiap sudut segi-n beraturan dapat ditentukan dengan rumus :
Jumlah besar setiap sudut segi-n : (n-2) x 180°
n
contoh :
- Jumlah besar setiap sudut segitiga =(3-2) x 180°=60°
3- Jumlah besar setiap sudut segiempat = (4-2) x 180°=90°
4
- Jumlah besar setiap sudut segilima =(5-2) x 180°=108°
5
Segi-n beraturan dalam lingkaran :
Setiap sudut dalam segi-n beraturan akan dilalui oleh lingkaran yang disebut lingkaran luar. setiap sudutnya menyentuh lingkaran luar tersebut. Setiap segi-n beraturan dapat dibagi menjadi n buah segitiga yang kongruen.
Sudut dalam segitiga dalam pada segi-n beraturan dapat dihitung dengan rumus:
Besar sudut dalam segitiga pada segi-n (α)=360/n
Menghitung luas segitiga dalam segi-n beraturan
Jika diketahui panjang jari-jari lingkaran dalam :
Luas segitiga dalam : ½ x r²x Sin α
Jika diketahui panjang sisi segi-n :
Luas segitiga dalam : s²x Sin²β
2 x Sin α
Dimana besar sudut β=180 - α
2
Menghitung luas segi-n beraturan
Karena segi-n beraturan terdiridari n buah segitiga yang kongruen, maka luas segi-n adalah n kali luas segitiga dalam tersebut.
Jika diketahui panjang jari-jari lingkaran dalam :
Luas segi-n : n x ½ x r²x Sin α
Jika diketahui panjang sisi segi-n :
Luas segi-n : n x s²x Sin²β
2 x Sin α
Berikut adalah contoh menghitung luas beberapa segi-n
Luas segilima beraturan
 |
| luas segi lima beraturan |
Jika diketahui panjang jari-jari lingkaran dalam :
Luas segilima : 5 x ½ x r²x Sin (360°/5)=5/2 x r²x Sin 72°
Jika diketahui panjang sisi segilima :
Luas segitiga dalam : 5 x s²x Sin²54°
2 x Sin 72°
Luas segienam beraturan
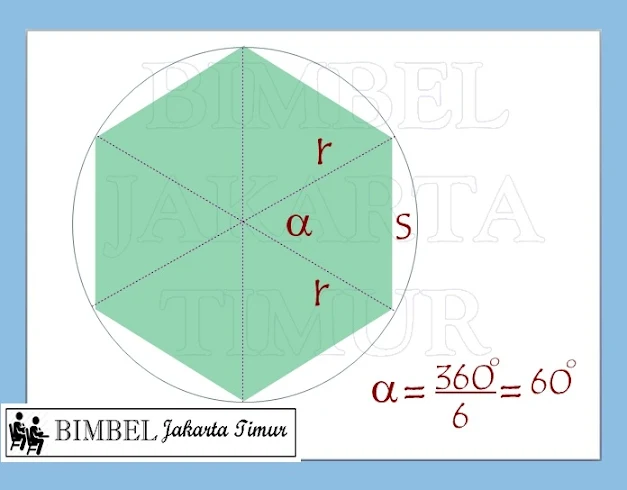 |
| segi enam beraturan |
Jika diketahui panjang jari-jari lingkaran dalam :
Luas segilima : 6 x ½ x r²x Sin (360°/6)=3 x r²x Sin 60°
Jika diketahui panjang sisi segienam :
Luas segienam : 6 x s²x Sin² 60° =3 x s²x Sin 60°
2 x Sin 60°
Luas segidelapan beraturan
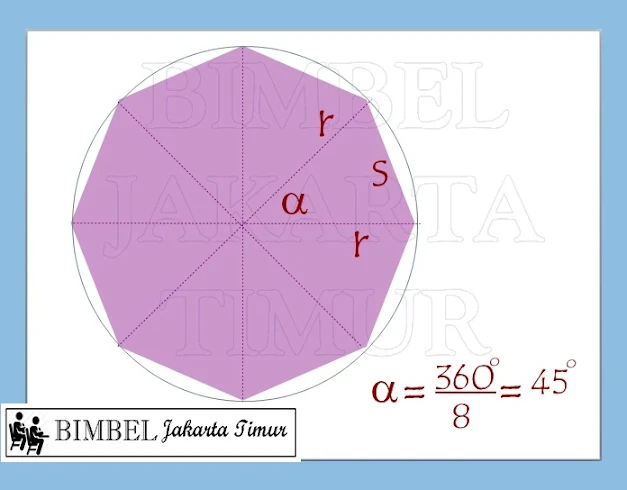 |
| luas segi delapan beraturan |
Jika diketahui panjang jari-jari lingkaran dalam :
Luas segilima : 8 x ½ x r²x Sin (360°/8)=4 x r²x Sin 45°
Jika diketahui panjang sisi segidelapan :
Luas segitiga dalam : 8 x s²x Sin²45° = 4 x s²x Sin²45°
2 x Sin 67,5° Sin 67,5°
BIMBEL JAKARTA TIMUR






0 Komentar